Open-loop optimal control¶
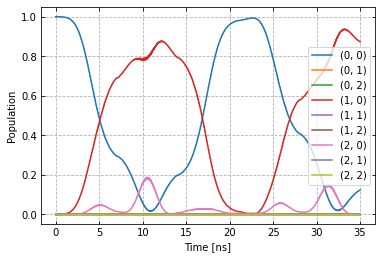
In order to improve the gate from the previous example Setup of a two-qubit chip with C^3, we create the optimizer object for open-loop optimal control. Examining the previous dynamics .. image:: dyn_singleX.png
in addition to over-rotation, we notice some leakage into the \(|2,0>\) state and enable a DRAG option. Details on DRAG can be found here. The main principle is adding a phase-shifted component proportional to the derivative of the original signal. With automatic differentiation, our AWG can perform this operation automatically for arbitrary shapes.
generator.devices['AWG'].enable_drag_2()
At the moment there are two implementations of DRAG, variant 2 is independent of the AWG resolution.
To define which parameters we optimize, we write the gateset_opt_map, a nested list of tuples that identifies each parameter.
opt_gates = ["rx90p[0]"]
gateset_opt_map=[
[
("rx90p[0]", "d1", "gauss", "amp"),
],
[
("rx90p[0]", "d1", "gauss", "freq_offset"),
],
[
("rx90p[0]", "d1", "gauss", "xy_angle"),
],
[
("RX90p:Id", "d1", "gauss", "delta"),
]
]
parameter_map.set_opt_map(gateset_opt_map)
We can look at the parameter values this opt_map specified with
parameter_map.print_parameters()
rx90p[0]-d1-gauss-amp : 500.000 mV
rx90p[0]-d1-gauss-freq_offset : -53.000 MHz 2pi
rx90p[0]-d1-gauss-xy_angle : -444.089 arad
rx90p[0]-d1-gauss-delta : -1.000
from c3.optimizers.optimalcontrol import OptimalControl
import c3.libraries.algorithms as algorithms
The OptimalControl object will handle the optimization for us. As a fidelity function we choose average fidelity as well as LBFG-S (a wrapper of the scipy implementation) from our library. See those libraries for how these functions are defined and how to supply your own, if necessary.
import os
import tempfile
# Create a temporary directory to store logfiles, modify as needed
log_dir = os.path.join(tempfile.TemporaryDirectory().name, "c3logs")
opt = OptimalControl(
dir_path=log_dir,
fid_func=fidelities.average_infid_set,
fid_subspace=["Q1", "Q2"],
pmap=parameter_map,
algorithm=algorithms.lbfgs,
options={"maxfun" : 10},
run_name="better_X90"
)
Finally we supply our defined experiment.
exp.set_opt_gates(opt_gates)
opt.set_exp(exp)
Everything is in place to start the optimization.
opt.optimize_controls()
After a few steps we have improved the gate significantly, as we can check with
opt.current_best_goal
0.00063
And by looking at the same sequences as before.
plot_dynamics(exp, init_state, barely_a_seq)
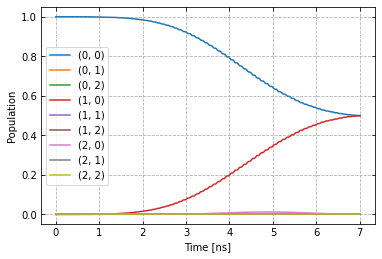
plot_dynamics(exp, init_state, barely_a_seq * 5)
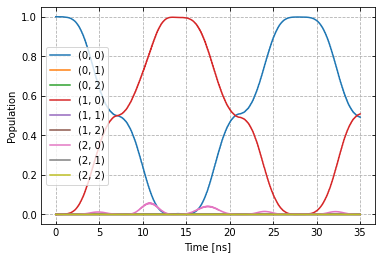
Compared to before the optimization.